A pilot’s ability to predict the performance of a helicopter is extremely important. It helps to determine how much weight the helicopter can carry before takeoff, if the helicopter can safely hover at a specific altitude and temperature, the distance required to climb above obstacles, and what the maximum climb rate will be.
Factors Affecting Performance
A helicopter’s performance is dependent on the power output of the engine and the lift produced by the rotors, whether it is the main rotor(s) or tail rotor. Any factor that affects engine and rotor efficiency affects performance. The three major factors that affect performance are density altitude, weight, and wind. The Aeronautical Knowledge section, discusses these factors in great detail.
Moisture (Humidity)
Humidity alone is usually not considered an important factor in calculating density altitude and helicopter performance; however, it does contribute. There are no rules of thumb used to compute the effects of humidity on density altitude, but some manufacturers include charts with 80 percent relative humidity columns as additional information. There appears to be an approximately 3–4 percent reduction in performance compared to dry air at the same altitude and temperature, so expect a decrease in hovering and takeoff performance in high humidity conditions. Although 3–4 percent seems insignificant, it can be the cause of a mishap when already operating at the limits of the helicopter.
Weight
Weight is one of the most important factors because the pilot can control it. Most performance charts include weight as one of the variables. By reducing the weight of the helicopter, a pilot may be able to take off or land safely at a location that otherwise would be impossible. However, if ever in doubt about whether a takeoff or landing can be performed safely, delay your takeoff until more favorable density altitude conditions exist. If airborne, try to land at a location that has more favorable conditions, or one where a landing can be made that does not require a hover.In addition, at higher gross weights, the increased power required to hover produces more torque, which means more antitorque thrust is required. In some helicopters during high altitude operations, the maximum antitorque produced by the tail rotor during a hover may not be sufficient to overcome torque even if the gross weight is within limits.
Winds
Wind direction and velocity also affect hovering, takeoff, and climb performance. Translational lift occurs any time there is relative airflow over the rotor disk. This occurs whether the relative airflow is caused by helicopter movement or by the wind. Assuming a headwind, as wind speed increases, translational lift increases, resulting in less power required to hover.
The wind direction is also an important consideration. Headwinds are the most desirable as they contribute to the greatest increase in performance. Strong crosswinds and tailwinds may require the use of more tail rotor thrust to maintain directional control. This increased tail rotor thrust absorbs power from the engine, which means there is less power available to the main rotor for the production of lift. Some helicopters even have a critical wind azimuth or maximum safe relative wind chart. Operating the helicopter beyond these limits could cause loss of tail rotor effectiveness.
Takeoff and climb performance is greatly affected by wind. When taking off into a headwind, effective translational lift is achieved earlier, resulting in more lift and a steeper climb angle. When taking off with a tailwind, more distance is required to accelerate through translation lift.
Performance Charts
In developing performance charts, aircraft manufacturers make certain assumptions about the condition of the helicopter and the ability of the pilot. It is assumed that the helicopter is in good operating condition, calm wind, and the engine is developing its rated power. The pilot is assumed to be following normal operating procedures and to have average flying abilities. Average means a pilot capable of doing each of the required tasks correctly and at the appropriate times.
Using these assumptions, the manufacturer develops performance data for the helicopter based on actual flight tests. However, they do not test the helicopter under each and every condition shown on a performance chart. Instead, they evaluate specific data and mathematically derive the remaining data.
Height/Velocity Diagram
The height/velocity (H/V) diagram shows the combinations of airspeed and height above the ground, which will allow an average pilot to successfully complete a landing after an engine failure. By carefully studying the height/velocity diagram, a pilot is able to avoid the combinations of altitude and airspeed that may not allow sufficient time or altitude to enter a stabilized autorotative descent. Refer to Figure 1 during the remainder of the discussion on the height/velocity diagram.
 |
| Figure 1. Sample height/velocity diagram for a Robinson Model R44 II |
In the simplest explanation, the H/V diagram is a diagram in which the shaded areas should be avoided, as the pilot may be unable to complete an autorotation landing without damage. The H/V diagram usually contains a takeoff profile, where the diagram can be traversed from zero height and zero speed to cruise, without entering the shaded areas or with minimum exposure to shaded areas.The grey portion on the left side of the diagram marks a flight profile that probably does not allow the pilot to complete an autorotation successfully, primarily due to having insufficient airspeed to enter an autorotative profile in time to avoid a crash. The shaded area on the lower right is dangerous due to the airspeed and proximity to the ground resulting in dramatically reduced reaction time for the pilot in the case of mechanical failure, or other in-flight emergencies. This shaded area at the lower right is not portrayed in H/V diagrams for multiengine helicopters capable of safely hovering and flying with a single engine failure.
The following examples further illustrate the relevance of the H/V diagram to a single-engine helicopter.
At low heights with low airspeed, such as a hover taxi, the pilot can simply use the kinetic energy from the rotor disk to cushion the landing with collective, converting rotational inertia to lift. The aircraft is in a safe part of the H/V diagram. At the extreme end of the scale (e.g., a three-foot hover taxi at walking pace) even a complete failure to recognize the power loss resulting in an uncushioned landing would probably be survivable.
As the airspeed increases without an increase in height, there comes a point at which the pilot’s reaction time would be insufficient to react with a flare in time to prevent a high speed, and thus probably fatal, ground impact. Another thing to consider is the length of the tailboom and the response time of the helicopter flight controls at slow airspeeds and low altitudes. Even small increases in height give the pilot much greater time to react; therefore, the bottom right part of the H/V diagram is usually a shallow gradient. If airspeed is above ideal autorotation speed, the pilot’s instinct is usually to flare to convert speed to height and increase rotor rpm through coning, which also immediately gets them out of the dead man’s curve.
Conversely, an increase in height without a corresponding increase in airspeed puts the aircraft above a survivable uncushioned impact height, and eventually above a height where rotor inertia can be converted to sufficient lift to enable a survivable landing. This occurs abruptly with airspeeds much below the ideal autorotative speed (typically 40–80 knots). The pilot must have enough time to accelerate to autorotation speed in order to autorotate successfully; this directly relates to a requirement for height. Above a certain height the pilot can achieve autorotation speed even from a zero knot start, thus putting high OGE hovers outside the curve.The typical safe takeoff profile involves initiation of forward flight from a 2–3 feet landing gear height, only gaining altitude as the helicopter accelerates through translational lift, as airspeed approaches a safe autorotative speed. At this point, some of the increased thrust available may be used to attain safe climb airspeed, which will keep the helicopter out of the shaded or hatched areas of the H/V diagram. Although helicopters are not restricted from conducting maneuvers that will place them in the shaded area of the H/V diagram, it is important for pilots to understand that operation in those shaded areas exposes pilot, aircraft, and passengers to a certain hazard should the engine or driveline malfunction. The pilot should always evaluate the risk of the maneuver versus the operational value.
The Effect of Weight Versus Density Altitude
The height/velocity diagram [Figure 1] depicts altitude and airspeed situations from which a successful autorotation can be made. The time required, and therefore, altitude necessary to attain a steady state autorotative descent, is dependent on the weight of the helicopter and the density altitude. For this reason, the H/V diagram is valid only when the helicopter is operated in accordance with the gross weight versus density altitude chart. If published, this chart is found in the RFM for the particular helicopter. [Figure 2] The gross weight versus density altitude chart is not intended to provide a restriction to gross weight, but to be an advisory of the autorotative capability of the helicopter during takeoff and climb. A pilot must realize, however, that at gross weights above those recommended by the gross weight versus density altitude chart, the values are unknown.
 |
| Figure 2. Gross weight versus density altitude |
Assuming a density altitude of 8,500 feet, the height/velocity diagram in Figure 1 would be valid up to a gross weight of approximately 2,500 pounds. This is found by entering the graph in Figure 2 at a density altitude of 8,500 feet (point A), then moving horizontally to the solid line (point B). Moving vertically to the bottom of the graph (point C), with the existing density altitude, the maximum gross weight under which the height/velocity diagram is applicable is 2,500 pounds.The production of performance charts and diagrams for helicopters are regulatory as set out in Title 14 of the Code of Federal Regulations (14 CFR) Part 27, Airworthiness Standards. These charts establish safer parameters for operation. Although not regulatory, the pilot should carry out a full risk assessment to carefully consider the higher risk before operating within the shaded areas of the height/ velocity diagram.
Autorotational Performance
Most autorotational performance charts state that autorotational descent performance is a function of indicated airspeed (IAS) and is essentially unaffected by density altitude and gross weight. Keep in mind that, at some point, the potential energy expended during the autorotation is converted into kinetic energy for the flare and touchdown phase of the maneuver. It is at that point that increased density altitudes and heavier gross weights have a great impact on the successful completion of the autorotation. The rotor disk must be able to overcome the downward momentum of the helicopter and provide enough lift to cushion the landing. With increased density altitudes and gross weights, the lift potential is reduced and a higher collective pitch angle (angle of incidence) is required.
During autorotation gravity provides the source of energy powering the rotor by causing upflow up through the rotor during descent. This is the same as saying that potential energy is being traded for kinetic energy to turn the rotor as the aircraft descends.
In Figure 3, the S-300 curve shows the various combinations of horizontal and vertical speeds that supply the required energy to keep the rotor turning at a constant 471 rpm. For example, an airspeed of 54 mph with a corresponding vertical speed of 1,600 feet per minute (fpm) will provide enough kinetic energy to maintain the rotor at a 471 rpm. The rotor does not care if the air is coming from the front or the bottom so long as the total is sufficient to maintain the rpm. Any point on the curve will maintain rotor speed. However, the pilot does care because if he or she, for example, glides at 30 knots, the corresponding rate of descent will be over 2,200 fpm. Since there is little airspeed for a deceleration (or “flare”) to reduce the rate of decent before touchdown, the collective pitch application (increasing blade pitch and giving a final temporary increase in lift before the blades slow down) may be insufficient to arrest the rate of descent.
 |
| Figure 3. An autorotation curve for the S-300 shows the various combinations of horizontal and vertical speeds that supply the required energy to keep the rotor turning at a constant 471 rpm |
Students who fully comprehend this relationship understand why training autorotations are usually limited to airspeeds between the minimum rate of descent airspeed and the maximum range airspeed (usually about 25 percent faster than the minimum rate of descent airspeed).
Referencing a curve similar to the one shown in Figure 3 is useful to understand the consequences of not maintaining the target airspeed when executing an autorotation. Simply put, the pilot should know why airspeed is the most significant factor affecting the rate of descent.
Hovering Performance
Helicopter performance revolves around whether or not the helicopter can be hovered. More power is required during the hover than in any other flight regime. Obstructions aside, if a hover can be maintained, a takeoff can be made, especially with the additional benefit of translational lift. Hover charts are provided for in ground effect (IGE) hover and out of ground effect (OGE) hover under various conditions of gross weight, altitude, temperature, and power. The IGE hover ceiling is usually higher than the OGE hover ceiling because of the added lift benefit produced by ground effect. See Aerodynamics of Flight section, for more details on IGE and OGE hover. A pilot should always plan an OGE hover when landing in an area that is uncertain or unverified.
As density altitude increases, more power is required to hover. At some point, the power required is equal to the power available. This establishes the hovering ceiling under the existing conditions. Any adjustment to the gross weight by varying fuel, payload, or both, affects the hovering ceiling. The heavier the gross weight, the lower the hovering ceiling. As gross weight is decreased, the hover ceiling increases.
Sample Hover Problem 1
You are to fly a photographer to a remote location to take pictures of the local wildlife.
 |
| Figure 4. In ground effect hovering ceiling versus gross weight chart |
Using Figure 4, can you safely hover in ground effect at your departure point with the following conditions?A. Pressure Altitude: 8,000 feet
B. Temperature: +15 °C
C. Takeoff Gross Weight:1,250 lb
rpm:104 percent
First enter the chart at 8,000 feet pressure altitude (point A), then move right until reaching a point midway between the +10 °C and +20 °C lines (point B). From that point, proceed down to find the maximum gross weight where a 2 foot hover can be achieved. In this case, it is approximately 1,280 pounds (point C).
Since the gross weight of your helicopter is less than this, you can safely hover with these conditions.
Sample Hover Problem 2
Once you reach the remote location in the previous problem, you will need to hover OGE for some of the pictures. The pressure altitude at the remote site is 9,000 feet, and you will use 50 pounds of fuel getting there. (The new gross weight is now 1,200 pounds.) The temperature will remain at +15 °C.
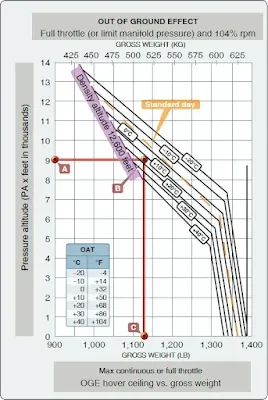 |
| Figure 5. Out of ground effect hover ceiling versus gross weight chart |
Using Figure 5, can you accomplish the mission?Enter the chart at 9,000 feet (point A) and proceed to point B (+15 °C). From there, determine that the maximum gross weight to hover OGE is approximately 1,130 pounds (point C). Since your gross weight is higher than this value, you will not be able to hover in these conditions. To accomplish the mission, you will need to remove approximately 70 pounds before you begin the flight.
These two sample problems emphasize the importance of determining the gross weight and hover ceiling throughout the entire flight operation. Being able to hover at the takeoff location with a specific gross weight does not ensure the same performance at the landing point. If the destination point is at a higher density altitude because of higher elevation, temperature, and/or relative humidity, more power is required to hover there. You should be able to predict whether hovering power will be available at the destination by knowing the temperature and wind conditions, using the performance charts in the helicopter flight manual, and making certain power checks during hover and in flight prior to commencing the approach and landing.
For helicopters with dual engines, performance charts provide torque amounts for both engines.
Sample Hover Problem 3
Using Figure 6, determine what torque is required to hover.
 |
| Figure 6. Torque required for cruise or level flight |
Use the following conditions:
A. Pressure Altitude: 9,500 feet
B. Outside Air Temperature.: 0 °C
C. Gross Weight: 4,250 lb
D. Desired Skid Height: 5 feetFirst, enter the chart at 9,500 feet pressure altitude, then move right to outside air temperature, 0 °C. From that point, move down to 4,250 pounds gross weight and then move left to 5-foot skid height. Drop down to read 66 percent torque required to hover.
Climb Performance
Most of the factors affecting hover and takeoff performance also affect climb performance. In addition, turbulent air, pilot techniques, and overall condition of the helicopter can cause climb performance to vary.
A helicopter flown at the best rate-of-climb speed (VY) obtains the greatest gain in altitude over a given period of time. This speed is normally used during the climb after all obstacles have been cleared and is usually maintained until reaching cruise altitude. Rate of climb must not be confused with angle of climb. Angle of climb is a function of altitude gained over a given distance. The VY results in the highest climb rate, but not the steepest climb angle, and may not be sufficient to clear obstructions. The best angle of climb speed (VX) depends upon the power available. If there is a surplus of power available, the helicopter can climb vertically, so VX is zero.
Wind direction and speed have an effect on climb performance, but it is often misunderstood. Airspeed is the speed at which the helicopter is moving through the atmosphere and is unaffected by wind. Atmospheric wind affects only the groundspeed, or speed at which the helicopter is moving over the Earth’s surface. Thus, the only climb performance affected by atmospheric wind is the angle of climb and not the rate of climb.
When planning for climb performance, it is first important to plan for torque settings at level flight. Climb performance charts show the change in torque, above or below torque, required for level flight under the same gross weight and atmospheric conditions to obtain a given rate of climb or descent.
Sample Cruise or Level Flight Problem
Determine torque setting for cruise or level flight using Figure 7.
 |
| Figure 7. Maximum rate-of-climb chart |
Use the following conditions:
Pressure Altitude: 8,000 feet
Outside Air Temperature: +15 °C
A. Indicated Airspeed: 80 knots
B. Maximum Gross Weight: 5,000 lbWith this chart, first confirm that it is for a pressure altitude of 8,000 feet with an OAT of 15°. Begin on the left side at 80 knots indicated airspeed (point A) and move right to maximum gross weight of 5,000 lb (point B). From that point, proceed down to the torque reading for level flight, which is 74 percent torque (point C). This torque setting is used in the next problem to add or subtract cruise/descent torque percentage from cruise flight.
Sample Climb Problem
Determine climb/descent torque percentage using Figure 8.
 |
| Figure 8. Climb/descent torque percentage chart |
Use the following conditions:
A. Rate of Climb or Descent: 500 fpm
B. Maximum Gross Weight: 5,000 lb
With this chart, first locate a 500-fpm rate of climb or descent (point A), and then move to the right to a maximum gross weight of 5,000 lb (point B). From that point, proceed down to the torque percentage, which is 15 percent torque (point C). For climb or descent, 15 percent torque should be added/subtracted from the 74 percent torque needed for level flight. For example, if the numbers were to be used for a climb torque, the pilot would adjust torque settings to 89 percent for optimal climb performance.
