Performance charts allow a pilot to predict the takeoff, climb, cruise, and landing performance of an aircraft. These charts, provided by the manufacturer, are included in the AFM/POH. Information the manufacturer provides on these charts has been gathered from test flights conducted in a new aircraft, under normal operating conditions while using average piloting skills, and with the aircraft and engine in good working order. Engineers record the flight data and create performance charts based on the behavior of the aircraft during the test flights. By using these performance charts, a pilot can determine the runway length needed to take off and land, the amount of fuel to be used during flight, and the time required to arrive at the destination. It is important to remember that the data from the charts will not be accurate if the aircraft is not in good working order or when operating under adverse conditions. Always consider the necessity to compensate for the performance numbers if the aircraft is not in good working order or piloting skills are below average.
Each aircraft performs differently and, therefore, has different performance numbers. Compute the performance of the aircraft prior to every flight, as every flight is different. (See appendix for examples of performance charts for a Cessna Model 172R and Challenger 605.)
Every chart is based on certain conditions and contains notes on how to adapt the information for flight conditions. It is important to read every chart and understand how to use it. Read the instructions provided by the manufacturer. For an explanation on how to use the charts, refer to the example provided by the manufacturer for that specific chart. [Figure 1]
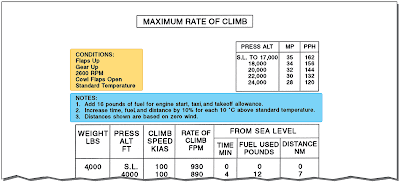 |
| Figure 1. Conditions notes chart |
The information manufacturers furnish is not standardized. Information may be contained in a table format and other information may be contained in a graph format. Sometimes combined graphs incorporate two or more graphs into one chart to compensate for multiple conditions of flight. Combined graphs allow the pilot to predict aircraft performance for variations in density altitude, weight, and winds all on one chart. Because of the vast amount of information that can be extracted from this type of chart, it is important to be very accurate in reading the chart. A small error in the beginning can lead to a large error at the end.
The remainder of this section covers performance information for aircraft in general and discusses what information the charts contain and how to extract information from the charts by direct reading and interpolation methods. Every chart contains a wealth of information that should be used when flight planning. Examples of the table, graph, and combined graph formats for all aspects of flight are discussed.
Interpolation
Not all of the information on the charts is easily extracted. Some charts require interpolation to find the information for specific flight conditions. Interpolating information means that by taking the known information, a pilot can compute intermediate information. However, pilots sometimes round off values from charts to a more conservative figure.
Using values that reflect slightly more adverse conditions provides a reasonable estimate of performance information and gives a slight margin of safety. The following illustration is an example of interpolating information from a takeoff distance chart. [Figure 2]
 |
| Figure 2. Interpolating charts |
Density Altitude Charts
Use a density altitude chart to figure the density altitude at the departing airport. Using Figure 3, determine the density altitude based on the given information.
 |
| Figure 3. Density altitude chart |
Sample Problem 1
Airport Elevation……………………5,883 feet
OAT……………………………………..70 °F
Altimeter……………………………….30.10 “Hg
First, compute the pressure altitude conversion. Find 30.10 under the altimeter heading. Read across to the second column. It reads “–165.” Therefore, it is necessary to subtract 165 from the airport elevation giving a pressure altitude of 5,718 feet. Next, locate the outside air temperature on the scale along the bottom of the graph. From 70°, draw a line up to the 5,718 feet pressure altitude line, which is about two-thirds of the way up between the 5,000 and 6,000 foot lines. Draw a line straight across to the far left side of the graph and read the approximate density altitude. The approximate density altitude in thousands of feet is 7,700 feet.
Takeoff Charts
Takeoff charts are typically provided in several forms and allow a pilot to compute the takeoff distance of the aircraft with no flaps or with a specific flap configuration. A pilot can also compute distances for a no flap takeoff over a 50 foot obstacle scenario, as well as with flaps over a 50 foot obstacle. The takeoff distance chart provides for various aircraft weights, altitudes, temperatures, winds, and obstacle heights.
Sample Problem 2
Pressure Altitude……………….2,000 feet
OAT…………………………………22 °C
Takeoff Weight………………….2,600 pounds
Headwind…………………………6 knots
Obstacle Height………………..50 foot obstacle
Refer to Figure 4. This chart is an example of a combined takeoff distance graph. It takes into consideration pressure altitude, temperature, weight, wind, and obstacles all on one chart. First, find the correct temperature on the bottom left side of the graph. Follow the line from 22 °C straight up until it intersects the 2,000 foot altitude line. From that point, draw a line straight across to the first dark reference line. Continue to draw the line from the reference point in a diagonal direction following the surrounding lines until it intersects the corresponding weight line. From the intersection of 2,600 pounds, draw a line straight across until it reaches the second reference line. Once again, follow the lines in a diagonal manner until it reaches the six knot headwind mark. Follow straight across to the third reference line and from here, draw a line in two directions. First, draw a line straight across to figure the ground roll distance. Next, follow the diagonal lines again until they reach the corresponding obstacle height. In this case, it is a 50 foot obstacle. Therefore, draw the diagonal line to the far edge of the chart. This results in a 700 foot ground roll distance and a total distance of 1,400 feet over a 50 foot obstacle. To find the corresponding takeoff speeds at lift-off and over the 50 foot obstacle, refer to the table on the top of the chart. In this case, the lift-off speed at 2,600 pounds would be 63 knots and over the 50 foot obstacle would be 68 knots.
 |
| Figure 4. Takeoff distance graph |
Sample Problem 3
Pressure Altitude………………3,000 feet
OAT………………………………..30 °C
Takeoff Weight…………………2,400 pounds
Headwind………………………..18 knots
Refer to Figure 5. This chart is an example of a takeoff distance table for short-field takeoffs. For this table, first find the takeoff weight. Once at 2,400 pounds, begin reading from left to right across the table. The takeoff speed is in the second column and, in the third column under pressure altitude, find the pressure altitude of 3,000 feet. Carefully follow that line to the right until it is under the correct temperature column of 30 °C. The ground roll total reads 1,325 feet and the total required to clear a 50 foot obstacle is 2,480 feet. At this point, there is an 18 knot headwind. According to the notes section under point number two, decrease the distances by ten percent for each 9 knots of headwind. With an 18 knot headwind, it is necessary to decrease the distance by 20 percent. Multiply 1,325 feet by 20 percent (1,325 × .20 = 265), subtract the product from the total distance (1,325 – 265 = 1,060). Repeat this process for the total distance over a 50 foot obstacle. The ground roll distance is 1,060 feet and the total distance over a 50 foot obstacle is 1,984 feet.
 |
| Figure 5. Takeoff distance short field charts |
Climb and Cruise Charts
Climb and cruise chart information is based on actual flight tests conducted in an aircraft of the same type. This information is extremely useful when planning a cross-country flight to predict the performance and fuel consumption of the aircraft. Manufacturers produce several different charts for climb and cruise performance. These charts include everything from fuel, time, and distance to climb to best power setting during cruise to cruise range performance.
The first chart to check for climb performance is a fuel, time, and distance-to-climb chart. This chart gives the fuel amount used during the climb, the time it takes to accomplish the climb, and the ground distance that is covered during the climb. To use this chart, obtain the information for the departing airport and for the cruise altitude. Using Figure 6, calculate the fuel, time, and distance to climb based on the information provided.
 |
| Figure 6. Fuel, time, and distance climb chart |
Sample Problem 4
Departing Airport Pressure Altitude…………..6,000 feet
Departing Airport OAT…………………………….25 °C
Cruise Pressure Altitude…………………………..10,000 feet
Cruise OAT…………………………………………….10 °C
First, find the information for the departing airport. Find the OAT for the departing airport along the bottom, left side of the graph. Follow the line from 25 °C straight up until it intersects the line corresponding to the pressure altitude of 6,000 feet. Continue this line straight across until it intersects all three lines for fuel, time, and distance. Draw a line straight down from the intersection of altitude and fuel, altitude and time, and a third line at altitude and distance. It should read three and one-half gallons of fuel, 6 minutes of time, and nine NM. Next, repeat the steps to find the information for the cruise altitude. It should read six gallons of fuel, 10.5 minutes of time, and 15 NM. Take each set of numbers for fuel, time, and distance and subtract them from one another (6.0 – 3.5 = 2.5 gallons of fuel). It takes two and one-half gallons of fuel and 4 minutes of time to climb to 10,000 feet. During that climb, the distance covered is six NM. Remember, according to the notes at the top of the chart, these numbers do not take into account wind, and it is assumed maximum continuous power is being used.
The next example is a fuel, time, and distance-to-climb table. For this table, use the same basic criteria as for the previous chart. However, it is necessary to figure the information in a different manner. Refer to Figure 7 to work the following sample problem.
 |
| Figure 7. Fuel time distance climb |
Sample Problem 5
Departing Airport Pressure Altitude…………Sea level
Departing Airport OAT…………………………..22 °C
Cruise Pressure Altitude…………………………8,000 feet
Takeoff Weight……………………………………..3,400 pounds
To begin, find the given weight of 3,400 in the first column of the chart. Move across to the pressure altitude column to find the sea level altitude numbers. At sea level, the numbers read zero. Next, read the line that corresponds with the cruising altitude of 8,000 feet. Normally, a pilot would subtract these two sets of numbers from one another, but given the fact that the numbers read zero at sea level, it is known that the time to climb from sea level to 8,000 feet is 10 minutes. It is also known that 21 pounds of fuel is used and 20 NM is covered during the climb. However, the temperature is 22 °C, which is 7° above the standard temperature of 15 °C. The notes section of this chart indicate that the findings must be increased by ten percent for each 7° above standard. Multiply the findings by ten percent or .10 (10 × .10 = 1, 1 + 10 = 11 minutes). After accounting for the additional ten percent, the findings should read 11 minutes, 23.1 pounds of fuel, and 22 NM. Notice that the fuel is reported in pounds of fuel, not gallons. Aviation fuel weighs six pounds per gallon, so 23.1 pounds of fuel is equal to 3.85 gallons of fuel (23.1 ÷ 6 = 3.85).
The next example is a cruise and range performance chart. This type of table is designed to give TAS, fuel consumption, endurance in hours, and range in miles at specific cruise configurations. Use Figure 8 to determine the cruise and range performance under the given conditions.
 |
| Figure 8. Cruise and range performance |
Sample Problem 6
Pressure Altitude…………………….5,000 feet
RPM……………………………………..2,400 rpm
Fuel Carrying Capacity……………38 gallons, no reserve
Find 5,000 feet pressure altitude in the first column on the left side of the table. Next, find the correct rpm of 2,400 in the second column. Follow that line straight across and read the TAS of 116 mph and a fuel burn rate of 6.9 gallons per hour. As per the example, the aircraft is equipped with a fuel carrying capacity of 38 gallons. Under this column, read that the endurance in hours is 5.5 hours and the range in miles is 635 miles.
Cruise power setting tables are useful when planning cross-country flights. The table gives the correct cruise power settings, as well as the fuel flow and airspeed performance numbers at that altitude and airspeed.
Sample Problem 7
Pressure Altitude at Cruise……………6,000 feet
OAT…………………………………………..36 °F above standard
Refer to Figure 9 for this sample problem. First, locate the pressure altitude of 6,000 feet on the far left side of the table. Follow that line across to the far right side of the table under the 20 °C (or 36 °F) column. At 6,000 feet, the rpm setting of 2,450 will maintain 65 percent continuous power at 21.0 “Hg with a fuel flow rate of 11.5 gallons per hour and airspeed of 161 knots.
 |
| Figure 9. Cruise power setting |
Another type of cruise chart is a best power mixture range graph. This graph gives the best range based on power setting and altitude. Using Figure 10, find the range at 65 percent power with and without a reserve based on the provided conditions.
 |
| Figure 10. Best power mixture range |
Sample Problem 8
OAT……………………………Standard
Pressure Altitude………….5,000 feet
First, move up the left side of the graph to 5,000 feet and standard temperature. Follow the line straight across the graph until it intersects the 65 percent line under both the reserve and no reserve categories. Draw a line straight down from both intersections to the bottom of the graph. At 65 percent power with a reserve, the range is approximately 522 miles. At 65 percent power with no reserve, the range should be 581 miles.
The last cruise chart referenced is a cruise performance graph. This graph is designed to tell the TAS performance of the airplane depending on the altitude, temperature, and power setting. Using Figure 11, find the TAS performance based on the given information.
 |
| Figure 11. Cruise performance graph |
Sample Problem 9
OAT………………………………16 °C
Pressure Altitude…………….6,000 feet
Power Setting…………………65 percent, best power
Wheel Fairings……………….Not installed
Begin by finding the correct OAT on the bottom left side of the graph. Move up that line until it intersects the pressure altitude of 6,000 feet. Draw a line straight across to the 65 percent, best power line. This is the solid line, that represents best economy. Draw a line straight down from this intersection to the bottom of the graph. The TAS at 65 percent best power is 140 knots. However, it is necessary to subtract 8 knots from the speed since there are no wheel fairings. This note is listed under the title and conditions. The TAS is 132 knots.
Crosswind and Headwind Component Chart
Every aircraft is tested according to Federal Aviation Administration (FAA) regulations prior to certification. The aircraft is tested by a pilot with average piloting skills in 90° crosswinds with a velocity up to 0.2 VS0 or two-tenths of the aircraft’s stalling speed with power off, gear down, and flaps down. This means that if the stalling speed of the aircraft is 45 knots, it must be capable of landing in a 9-knot, 90° crosswind. The maximum demonstrated crosswind component is published in the AFM/POH. The crosswind and headwind component chart allows for figuring the headwind and crosswind component for any given wind direction and velocity.
Sample Problem 10
Runway……………….17
Wind…………………..140° at 25 knots
Refer to Figure 12 to solve this problem. First, determine how many degrees difference there is between the runway and the wind direction. It is known that runway 17 means a direction of 170°; from that subtract the wind direction of 140°. This gives a 30° angular difference or wind angle. Next, locate the 30° mark and draw a line from there until it intersects the correct wind velocity of 25 knots. From there, draw a line straight down and a line straight across. The headwind component is 22 knots and the crosswind component is 13 knots. This information is important when taking off and landing so that, first of all, the appropriate runway can be picked if more than one exists at a particular airport, but also so that the aircraft is not pushed beyond its tested limits.
 |
| Figure 12. Crosswind component chart |
Landing Charts
Landing performance is affected by variables similar to those affecting takeoff performance. It is necessary to compensate for differences in density altitude, weight of the airplane, and headwinds. Like takeoff performance charts, landing distance information is available as normal landing information, as well as landing distance over a 50 foot obstacle. As usual, read the associated conditions and notes in order to ascertain the basis of the chart information. Remember, when calculating landing distance that the landing weight is not the same as the takeoff weight. The weight must be recalculated to compensate for the fuel that was used during the flight.
Sample Problem 11
Pressure Altitude………………1,250 feet
Temperature…………………….Standard
Refer to Figure 13. This example makes use of a landing distance table. Notice that the altitude of 1,250 feet is not on this table. It is, therefore, necessary to interpolate to find the correct landing distance. The pressure altitude of 1,250 is halfway between sea level and 2,500 feet. First, find the column for sea level and the column for 2,500 feet. Take the total distance of 1,075 for sea level and the total distance of 1,135 for 2,500 and add them together. Divide the total by two to obtain the distance for 1,250 feet. The distance is 1,105 feet total landing distance to clear a 50 foot obstacle. Repeat this process to obtain the ground roll distance for the pressure altitude. The ground roll should be 457.5 feet.
 |
| Figure 13. Landing distance table |
Sample Problem 12
OAT……………………………………. 57 °F
Pressure Altitude………………….. 4,000 feet
Landing Weight……………………..2,400 pounds
Headwind……………………………. 6 knots
Obstacle Height…………………… 50 feet
Using the given conditions and Figure 14, determine the landing distance for the aircraft. This graph is an example of a combined landing distance graph and allows compensation for temperature, weight, headwinds, tailwinds, and varying obstacle height. Begin by finding the correct OAT on the scale on the left side of the chart. Move up in a straight line to the correct pressure altitude of 4,000 feet. From this intersection, move straight across to the first dark reference line. Follow the lines in the same diagonal fashion until the correct landing weight is reached. At 2,400 pounds, continue in a straight line across to the second dark reference line. Once again, draw a line in a diagonal manner to the correct wind component and then straight across to the third dark reference line. From this point, draw a line in two separate directions: one straight across to figure the ground roll and one in a diagonal manner to the correct obstacle height. This should be 975 feet for the total ground roll and 1,500 feet for the total distance over a 50 foot obstacle.
 |
| Figure 14. Landing distance graph |
Stall Speed Performance Charts
Stall speed performance charts are designed to give an understanding of the speed at which the aircraft stalls in a given configuration. This type of chart typically takes into account the angle of bank, the position of the gear and flaps, and the throttle position. Use Figure 15 and the accompanying conditions to find the speed at which the airplane stalls.
 |
| Figure 15. Stall speed table |
Sample Problem 13
Power……………………………….. OFF
Flaps………………………………… Down
Gear…………………………………. Down
Angle of Bank…………………… 45°
First, locate the correct flap and gear configuration. The bottom half of the chart should be used since the gear and flaps are down. Next, choose the row corresponding to a power-off situation. Now, find the correct angle of bank column, which is 45°. The stall speed is 78 mph, and the stall speed in knots would be 68 knots.
Performance charts provide valuable information to the pilot. By using these charts, a pilot can predict the performance of the aircraft under most flying conditions, providing a better plan for every flight. The Code of Federal Regulations (CFR) requires that a pilot be familiar with all information available prior to any flight. Pilots should use the information to their advantage as it can only contribute to safety in flight.















