Weight and Balance Theory (Part 2)

Figure 1. Locating balance point with three weights

To shift weight B so the lever balances about its center, 50 inches from the CG of weight A, first determine the arm of weight B that produces a moment that causes the total moment of all three weights around this desired balance point to be zero. The combined moment of weights A and C around this new balance point is 5,000 lb-in, so the moment of weight B must be –5,000 lb-in for the lever to balance. [Figure 2]

Figure 2. Proving the new balance point is correct

Determine the arm of weight B by dividing its moment, –5,000 lb-in, by its weight of 200 pounds. The arm is –25 inches. To balance the lever at its center, weight B must be placed so its CG is 25 inches to the left of the center of the lever. [Figure 3]

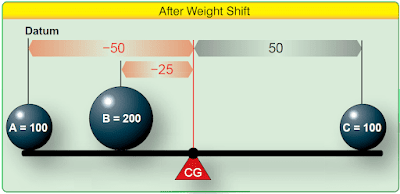Figure 3. Weight distribution to balance lever

Figure 4. Weight shift provides correct CG

Figure 4 indicates that the shift in weight depicted in Figure 3 allows the lever to balance as the sum of the moments is zero.

Basic Weight and Balance Equation

The following formulas can be used to determine the distance weight must be shifted to obtain a desired change in the CG location. The equation can also be rearranged to fid the amount of weight required to be shifted to move the CG to a desired location, to find the distance the CG is moved when a specified amount of weight is shifted, or to find the total weight that would allow shifting a specified amount of weight to move the CG a given distance.

Solution by Formula

The problem in Figure 1 can be solved by using variations of this basic equation. First, rearrange the formula to determine the distance weight B must be shifted:

The CG of the lever in Figure 1 was 72 inches from the datum. This CG can be shifted to the center of the lever as in Figure 3 by moving weight B. If the 200-pound weight B is moved 55 inches to the left, the CG shifts from +72 inches to +50 inches, a distance of 22 inches.

When the distance the weight is to be shifted is known, the amount of weight to be shifted to move the CG to any location can be determined by another arrangement of the basic equation. Use the following arrangement of the formula to determine the amount of weight that has to be shifted from station 8 to station +25, to move the CG from station +72 to station +50.

If the 200-pound weight B is shifted from station +80 to station +25, the CG moves from station +72 to station +50.

A third arrangement of this basic equation is used to determine the amount the CG is shifted when a given amount of weight is moved for a specified distance (as it was done in Figure 1). The following formula is used to determine the amount the CG is shifted when 200-pound weight B is moved from +80 to +25.

Moving weight B from +80 to +25 moves the CG 22 inches from its original location at +72 to its new location at +50 as seen in Figure 3.

To complete the calculations, return to the original formula and enter the appropriate numbers.

The equation is balanced.

Mean Aerodynamic Chord

The CG point affects the stability of the aircraft. To ensure the aircraft is safe to fly,the CG must fall within specified limits established by the manufacturer.

On some aircraft, the CG is expressed as a percentage of the length of the mean aerodynamic chord (MAC) or “percent MAC.” [Figure 5] In order to make such a calculation, the position of the leading edge of the MAC must be known ahead of time.

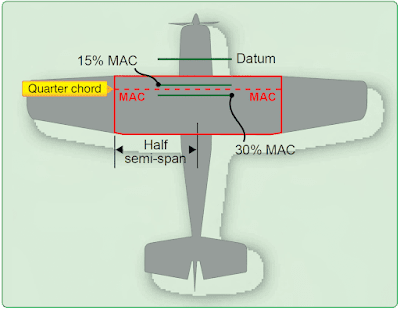Figure 5. Center of gravity expressed as percent mean aerodynamic chord

CG limits are specified forward and aft and/or lateral (left and right) limits within which the aircraft’s CG must be located during flight. The area between the limits is called the CG range of the aircraft.

The position of the fore and aft CG limits is measured as a percentage of MAC from the MAC leading edge. Usually for a single or two-seat aircraft, the most forward position would be forward of 30–35 percent MAC. Thus, the allowable CG range in a light aircraft should not exceed 20 percent MAC.

Note: For a rectangular width of constant airfoil section dimensions, MAC is just the chord. For a symmetrically-tapered wing, it is the average of the root chord and the tip chord.

FAA-Furnished Weight and Balance Information

The information discussed to this point can be readily applied to any aircraft weight and balance problem. To apply the techniques, certain elements of information are required. This information is obtained from both FAA documents and manufacturer provided data.

Before an aircraft CG can be computed, certain information must be known. This information, furnished by the FAA for every certificated aircraft in the Type Certificate Data Sheets (TCDS) or Aircraft Specifications, can be accessed at www.faa.gov. When the design of an aircraft is approved by the FAA, an Approved Type Certificate and TCDS are issued. The TCDS includes all of the pertinent specification for the aircraft; at each annual or 100-hour inspection, it is the responsibility of the inspecting mechanic or repairman to ensure that the aircraft adheres to them. A note about the TCDS: aircraft certificated before January 1, 1958, were issued Aircraft Specifications under the Civil Air Regulations (CARs), but when the Civil Aeronautical Administration (CAA) was replaced by the FAA, Aircraft Specification were replaced by the TCDS.

The weight and balance information on a TCDS includes CG range, empty weight CG range (EWCG), maximum weights, number of seats, maximum baggage, fuel capacity, oil capacity, and datum location. Data pertinent to an individual model is located in its respective section of the TCDS. Use the TCDS excerpts in Figure 6 to verify the following for a Cirrus Design Corporation SR 20 normal category:

Figure 6. Sample excerpt from TCDS A00009CH

Figure 6. Sample excerpt from TCDS A00009CH (Continued)

Figure 6. Sample excerpt from TCDS A00009CH (Continued)

Figure 6. Sample excerpt from TCDS A00009CH (Continued)

Figure 6. Sample excerpt from TCDS A00009CH (Continued)

CG Range

S/N 1005 through 1147:
Forward Limits: 138.7 inches at 2,110 lb with a straight line taper to 141.0 in at 2,694 lb and 143.0 in at 2,900 lb

Aft Limits: 144.6 in at 2,110 lb, with straight line taper to 147.4 in at 2,570 lb, and to 147.9 in at 2,745 lb, and 148.2 in at 2,900 lb

S/N 1148 through 1877, 1879 through 1885, and S/N 1005 through 1147 if Cirrus Service Bulletin SB 20-01-00 is complied with:
Forward Limits: 138.7 in at 2,110 lb with a straight line taper to 141.0 in at 2,694 lb and 144.1 in at 3,000 lb

Aft Limits: 144.6 in at 2,110 lb, with straight line taper to 147.4 in at 2,570 lb, and to 148.1 in at 2,900 lb, and 148.0 in at 3,000 lb

S/N 1878, 1886 and Subsequent:
Forward Limits: 137.8 in at 2,100 lb with a straight line taper to 139.1 in at 2,700 lb, and to 140.7 in at 3,050 lb

Aft Limits: 148.1 in at 2,100 lb, with straight line to 148.1 in at 3,050 lb

Maximum Weights

The maximum allowable takeoff and landing weights and the maximum allowable ramp weight are given. This basic information may be altered by a note. Notes are found in data pertinent to all models. An example would be Note 6 at the end of Figure 6.

Number of Seats

The number of seats and their arms are given in such terms as: 4 (2 at 143.5 aft of datum, 2 at 180 aft of datum).

Maximum Baggage

Maximum baggage for this model is 130 pounds at 208 inches.

Fuel Capacity

This important information is given in such terms as: 60.5 gal at 153.75 in. Usable: 56 gal (See Note 1). Notes can be found in data pertinent to all models.

Oil Capacity (Wet Sump)

The quantity of the full oil supply and its arm are given: 8 quarts at 76.2 in.

Data Pertinent to all Models

The location of the datum is specified and is described, for example, as: 100 inches in front of the forward face of the firewall bulkhead.