Once a helicopter leaves the ground, it is acted upon by four aerodynamic forces; thrust, drag, lift, and weight. Understanding how these forces work and knowing how to control them with the use of power and flight controls are essential to flight. [Figure 1]
They are defined as follows:
- Lift—opposes the downward force of weight, is produced by the dynamic effect of the air acting on the airfoil and acts perpendicular to the flightpath through the center of lift.
- Weight—the combined load of the aircraft itself, the crew, the fuel, and the cargo or baggage. Weight pulls the aircraft downward because of the force of gravity. It opposes lift and acts vertically downward through the aircraft’s center of gravity (CG).
- Thrust—the force produced by the power plant/ propeller or rotor. It opposes or overcomes the force of drag. As a general rule, it acts parallel to the longitudinal axis. However, this is not always the case, as explained later.
- Drag—a rearward, retarding force caused by disruption of airflow by the wing, rotor, fuselage, and other protruding objects. Drag opposes thrust and acts rearward parallel to the relative wind.
For a more in-depth explanation of general aerodynamics, refer to the Aeronautical Knowledge section.
Lift
Lift is generated when an object changes the direction of flow of a fluid or when the fluid is forced to move by the object passing through it. When the object and fluid move relative to each other and the object turns the fluid flow in a direction perpendicular to that flow, the force required to do this work creates an equal and opposite force that is lift. The object may be moving through a stationary fluid, or the fluid may be flowing past a stationary object—these two are effectively identical as, in principle, it is only the frame of reference of the viewer which differs. The lift generated by an airfoil depends on such factors as:
- Speed of the airflow
- Density of the air
- Total area of the segment or airfoil
- Angle of attack (AOA) between the air and the airfoil
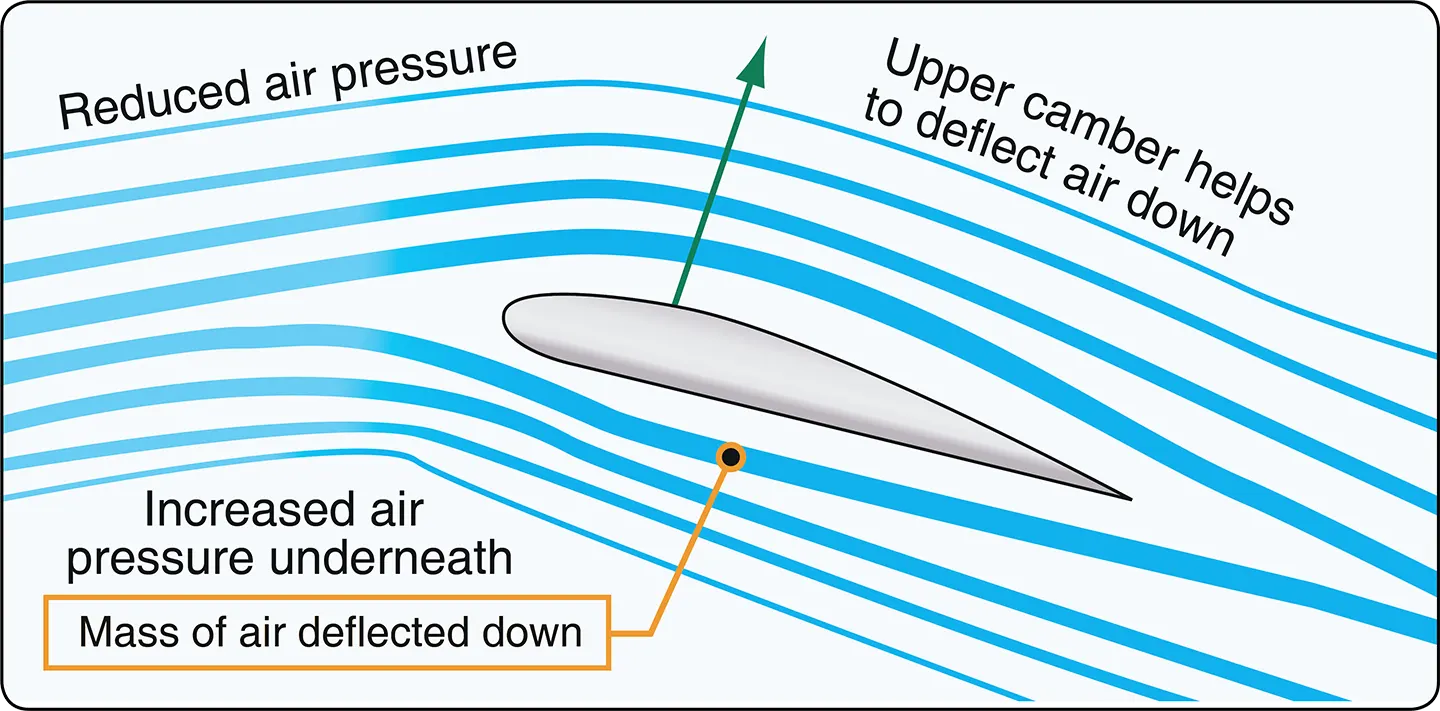
The AOA is the angle at which the airfoil meets the oncoming airflow (or vice versa). In the case of a helicopter, the object is the rotor blade (airfoil) and the fluid is the air. Lift is produced when a mass of air is deflected, and it always acts perpendicular to the resultant relative wind. A symmetric airfoil must have a positive AOA to generate positive lift. At a zero AOA, no lift is generated. At a negative AOA, negative lift is generated. A cambered or nonsymmetrical airfoil may produce positive lift at zero, or even small negative AOA.
The basic concept of lift is simple. However, the details of how the relative movement of air and airfoil interact to produce the turning action that generates lift are complex. In any case causing lift, an angled flat plate, revolving cylinder, airfoil, etc., the flow meeting the leading edge of the object is forced to split over and under the object. The sudden change in direction over the object causes an area of low pressure to form behind the leading edge on the upper surface of the object. In turn, due to this pressure gradient and the viscosity of the fluid, the flow over the object is accelerated down along the upper surface of the object. At the same time, the flow forced under the object is rapidly slowed or stagnated causing an area of high pressure. This also causes the flow to accelerate along the upper surface of the object. The two sections of the fluid each leave the trailing edge of the object with a downward component of momentum, producing lift. [Figure 2]
Bernoulli’s Principle
Bernoulli’s principle describes the relationship between internal fluid pressure and fluid velocity. It is a statement of the law of conservation of energy and helps explain why an airfoil develops an aerodynamic force. The concept of conservation of energy states energy cannot be created or destroyed and the amount of energy entering a system must also exit. Specifically, in this case the “energy” referred to is the dynamic pressure (the kinetic energy of the air— more velocity, more kinetic energy) and static air pressure (potential energy). These will change among themselves, but the total pressure energy remains constant inside the tube.
A simple tube with a constricted portion near the center of its length illustrates this principle. An example is running water through a garden hose. The mass of flow per unit area (cross-sectional area of tube) is the mass flow rate. In Figure 3, the flow into the tube is constant, neither accelerating nor decelerating; thus, the mass flow rate through the tube must be the same at stations 1, 2, and 3. If the cross-sectional area at any one of these stations—or any given point—in the tube is reduced, the fluid velocity must increase to maintain a constant mass flow rate to move the same amount of fluid through a smaller area. The continuity of mass flow causes the air to move faster through the venturi. In other words, fluid speeds up in direct proportion to the reduction in area.
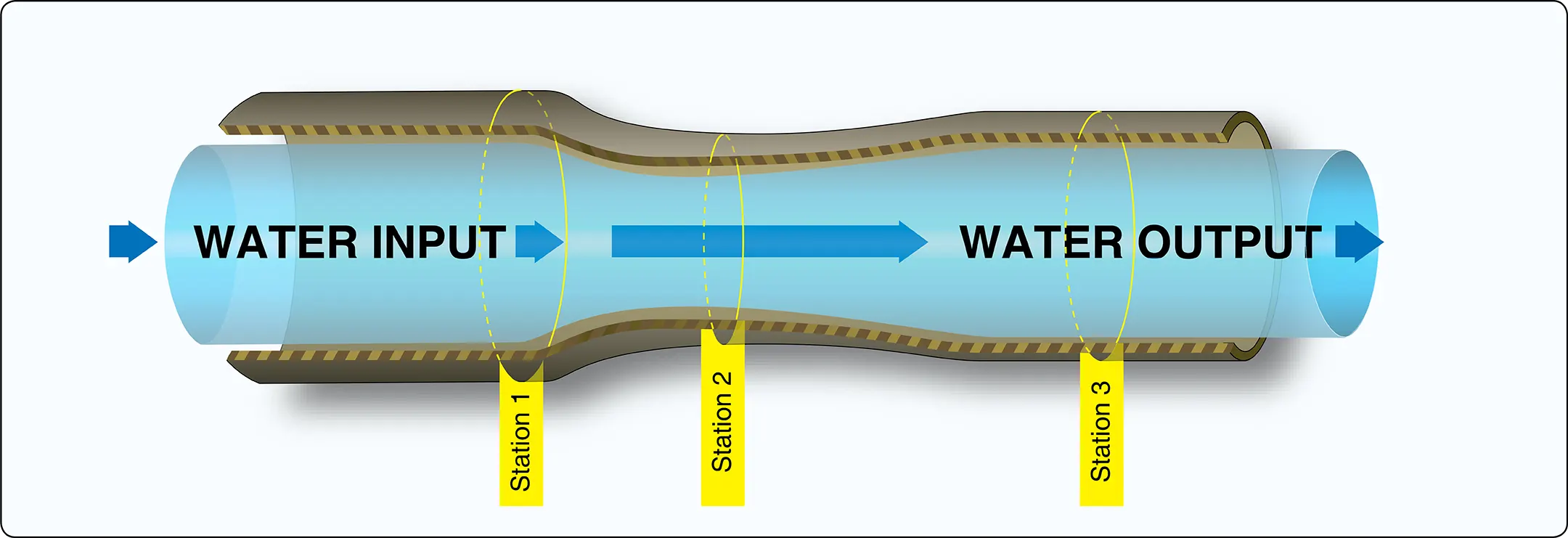
Bernoulli (Ptotal = Pdynamic + Pstatic) states that the increase in velocity will increase the streamwise dynamic pressure. Since the total pressure in the tube must remain constant, the static pressure on the sides of the venturi will decrease. Venturi effect is the term used to describe this phenomenon.
Figure 4 illustrates plates of one square foot in the dynamic flow and on the sides of the tube indicating static pressure, with corresponding pressure. At point 2, it is easier to visualize the static pressure reduction on the top of the airfoil as compared to the bottom of the airfoil, which is depicted as outside of the tube and therefore at ambient static pressure. Keep in mind with actual blades it is not a simple as this example because the bottom static pressure is influenced by blade design and blade angle, among other things. However, the basic idea is that it is the static pressure differential between the top and bottom multiplied by the surface area of the blade that generates the aerodynamic force.
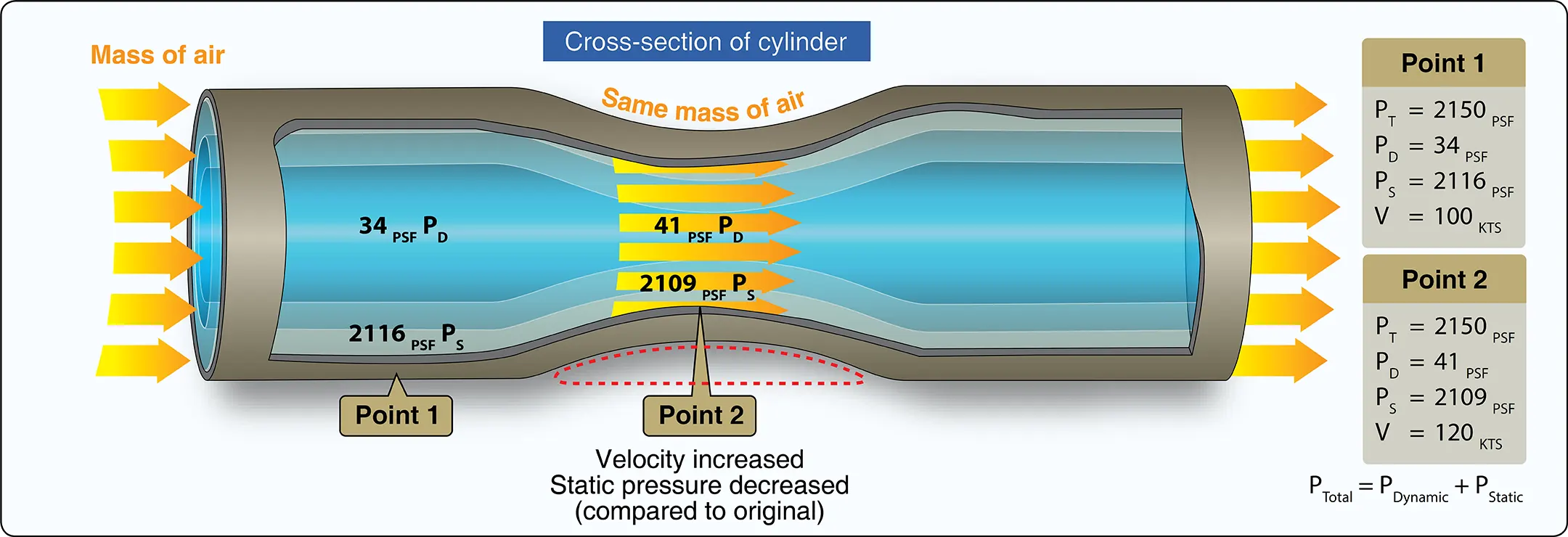
Venturi Flow
While the amount of total energy within a closed system (the tube) does not change, the form of the energy may be altered. Pressure of flowing air may be compared to energy in that the total pressure of flowing air always remains constant unless energy is added or removed. Fluid flow pressure has two components—static and dynamic pressure. Static pressure is the pressure component measured in the flow but not moving with the flow as pressure is measured. Static pressure is also known as the force per unit area acting on a surface. Dynamic pressure of flow is that component existing as a result of movement of the air. The sum of these two pressures is total pressure. As air flows through the constriction, static pressure decreases as velocity increases. This increases dynamic pressure.
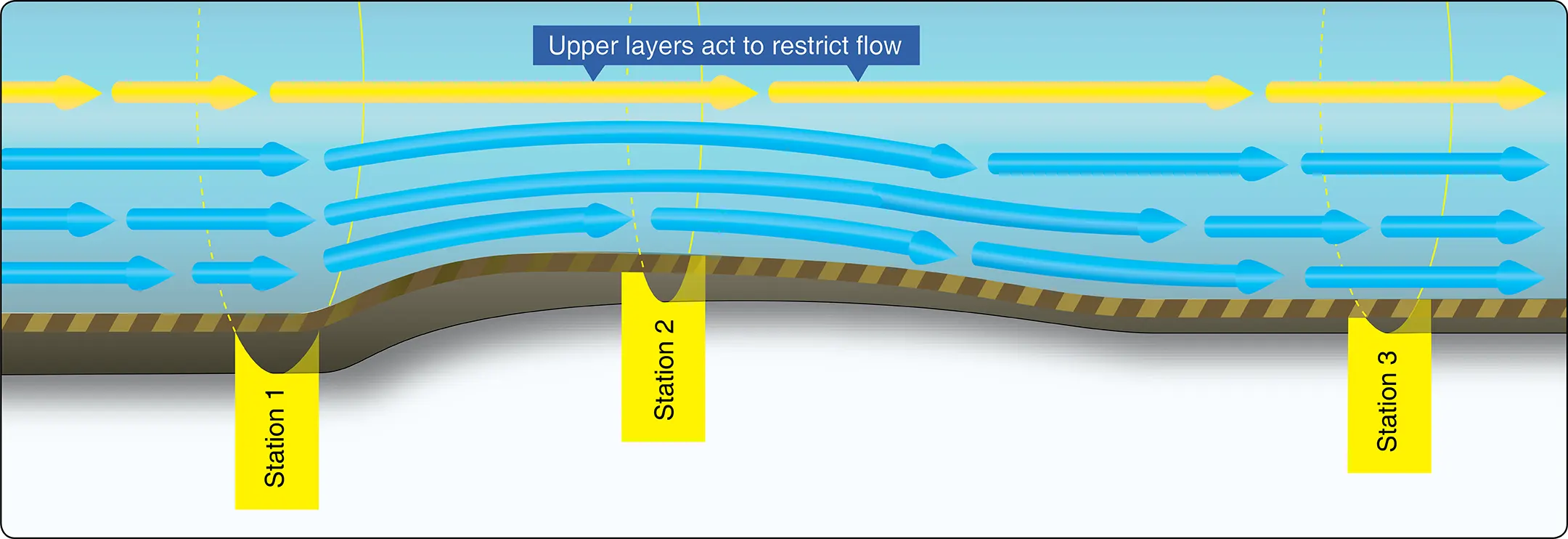
Figure 5 depicts the bottom half of the constricted area of the tube, which resembles the top half of an airfoil. Even with the top half of the tube removed, the air still accelerates over the curved area because the upper air layers restrict the flow—just as the top half of the constricted tube did. This acceleration causes decreased static pressure above the curved portion and creates a pressure differential caused by the variation of static and dynamic pressures.
Newton’s Third Law of Motion
Additional lift is provided by the rotor blade’s lower surface as air striking the underside is deflected downward. According to Newton’s Third Law of Motion, “for every action there is an equal and opposite reaction,” the air that is deflected downward also produces an upward (lifting) reaction.
ince air is much like water, the explanation for this source of lift may be compared to the planing effect of skis on water. The lift that supports the water skis (and the skier) is the force caused by the impact pressure and the deflection of water from the lower surfaces of the skis.
Under most flying conditions, the impact pressure and the deflection of air from the lower surface of the rotor blade provides a comparatively small percentage of the total lift. The majority of lift is the result of decreased pressure above the blade, rather than the increased pressure below it.
Weight
Normally, weight is thought of as being a known, fixed value, such as the weight of the helicopter, fuel, and occupants. To lift the helicopter off the ground vertically, the rotor disk must generate enough lift to overcome or offset the total weight of the helicopter and its occupants. Newton’s First Law states: “Every object in a state of uniform motion tends to remain in that state of motion unless an external force is applied to it.” In this case, the object is the helicopter whether at a hover or on the ground and the external force applied to it is lift, which is accomplished by increasing the pitch angle of the main rotor blades. This action forces the helicopter into a state of motion, without it the helicopter would either remain on the ground or at a hover.
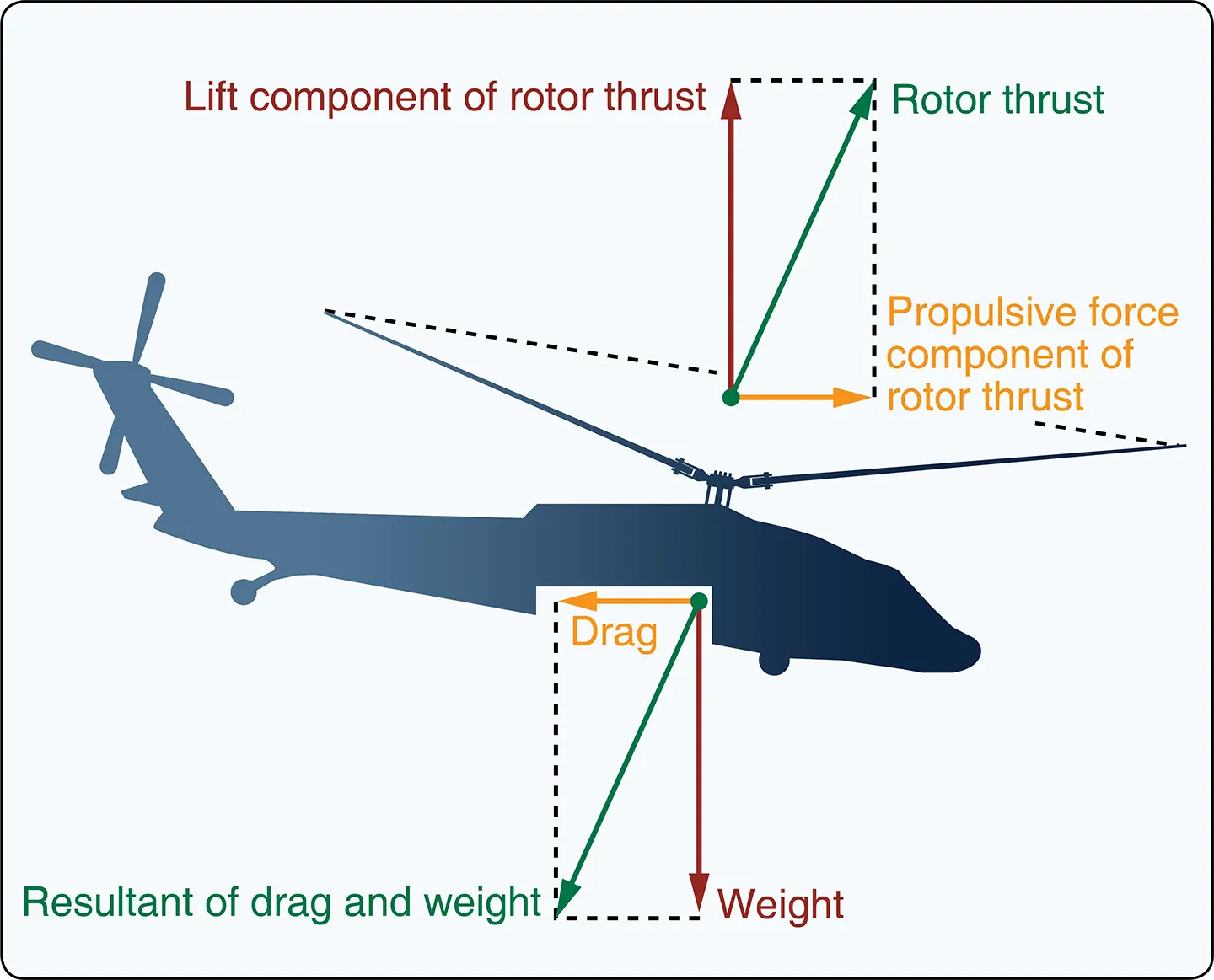
The weight of the helicopter can also be influenced by aerodynamic loads. When you bank a helicopter while maintaining a constant altitude, the “G” load or load factor increases. The load factor is the actual load on the rotor blades at any time, divided by the normal load or gross weight (weight of the helicopter and its contents). Any time a helicopter flies in a constant altitude curved flightpath, the load supported by the rotor blades is greater than the total weight of the helicopter. The tighter the curved flightpath is, the steeper the bank is; the more rapid the flare or pullout from a dive is, the greater the load supported by the rotor. Therefore, the greater the load factor must be. [Figure 6]
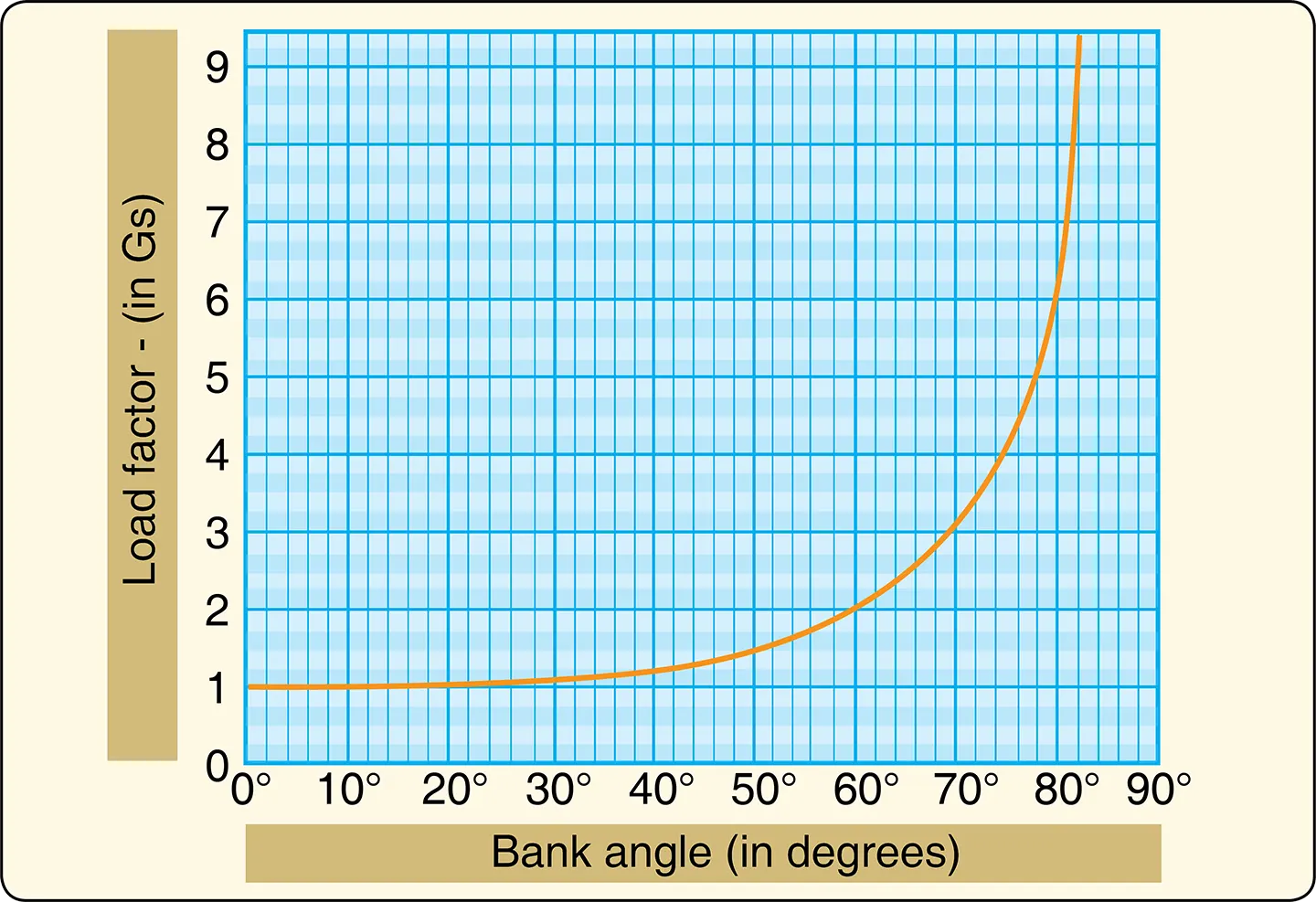
To overcome this additional load factor, the helicopter must be able to produce more lift. If excess engine power is not available, the helicopter either descends or has to decelerate in order to maintain the same altitude. The load factor and, hence, apparent gross weight increase is relatively small in banks up to 30°. Even so, under the right set of adverse circumstances, such as high-density altitude, turbulent air, high gross weight, and poor pilot technique, sufficient or excess power may not be available to maintain altitude and airspeed. Pilots must take all of these factors into consideration throughout the entire flight from the point of ascending to a hover to landing. Above 30° of bank, the apparent increase in gross weight soars. At 30° of bank, or pitch, the apparent increase is only 16 percent, but at 60°, it is twice the load on the wings and rotor disk.
For example, if the weight of the helicopter is 1,600 pounds, the weight supported by the rotor disk in a 30° bank at a constant altitude would be 1,856 pounds (1,600 + 16 percent (or 256)). In a 60° bank, it would be 3,200 pounds; in an 80° bank, it would be almost six times as much, or 8,000 pounds. It is important to note that each rotor blade must support a percentage of the gross weight. In a two-bladed system, each blade of the 1,600-pound helicopter as stated above would have to lift 50 percent or 800 pounds. If this same helicopter had three rotor blades, each blade would have to lift only 33 percent, or 533 pounds. One additional cause of large load factors is rough or turbulent air. The severe vertical gusts produced by turbulence can cause a sudden increase in AOA, resulting in increased rotor blade loads that are resisted by the inertia of the helicopter.
Each type of helicopter has its own limitations that are based on the aircraft structure, size, and capabilities. Regardless of how much weight one can carry or the engine power that it may have, they are all susceptible to aerodynamic overloading. Unfortunately, if the pilot attempts to push the performance envelope the consequence can be fatal. Aerodynamic forces effect every movement in a helicopter, whether it is increasing the collective or a steep bank angle. Anticipating results from a particular maneuver or adjustment of a flight control is not good piloting technique. Instead pilots need to truly understand the capabilities of the helicopter under any and all circumstances and plan never to exceed the flight envelope for any situation.
Thrust
Thrust, like lift, is generated by the rotation of the main rotor disk. In a helicopter, thrust can be forward, rearward, sideward, or vertical. The resultant lift and thrust determines the direction of movement of the helicopter.
The solidity ratio is the ratio of the total rotor blade area, which is the combined area of all the main rotor blades, to the total rotor disk area. This ratio provides a means to measure the potential for a rotor disk to provide thrust and lift. The mathematical calculations needed to calculate the solidity ratio for each helicopter may not be of importance to most pilots but what should be are the capabilities of the rotor disk to produce and maintain lift. Many helicopter accidents are caused from the rotor disk being overloaded. Simply put, pilots attempt maneuvers that require more lift than the rotor disk can produce or more power than the helicopter’s powerplant can provide. Trying to land with a nose high attitude along with any other unfavorable condition (i.e., high gross weight or wind gusts) is most likely to end in disaster.
The tail rotor also produces thrust. The amount of thrust is variable through the use of the antitorque pedals and is used to control the helicopter’s yaw.
Drag
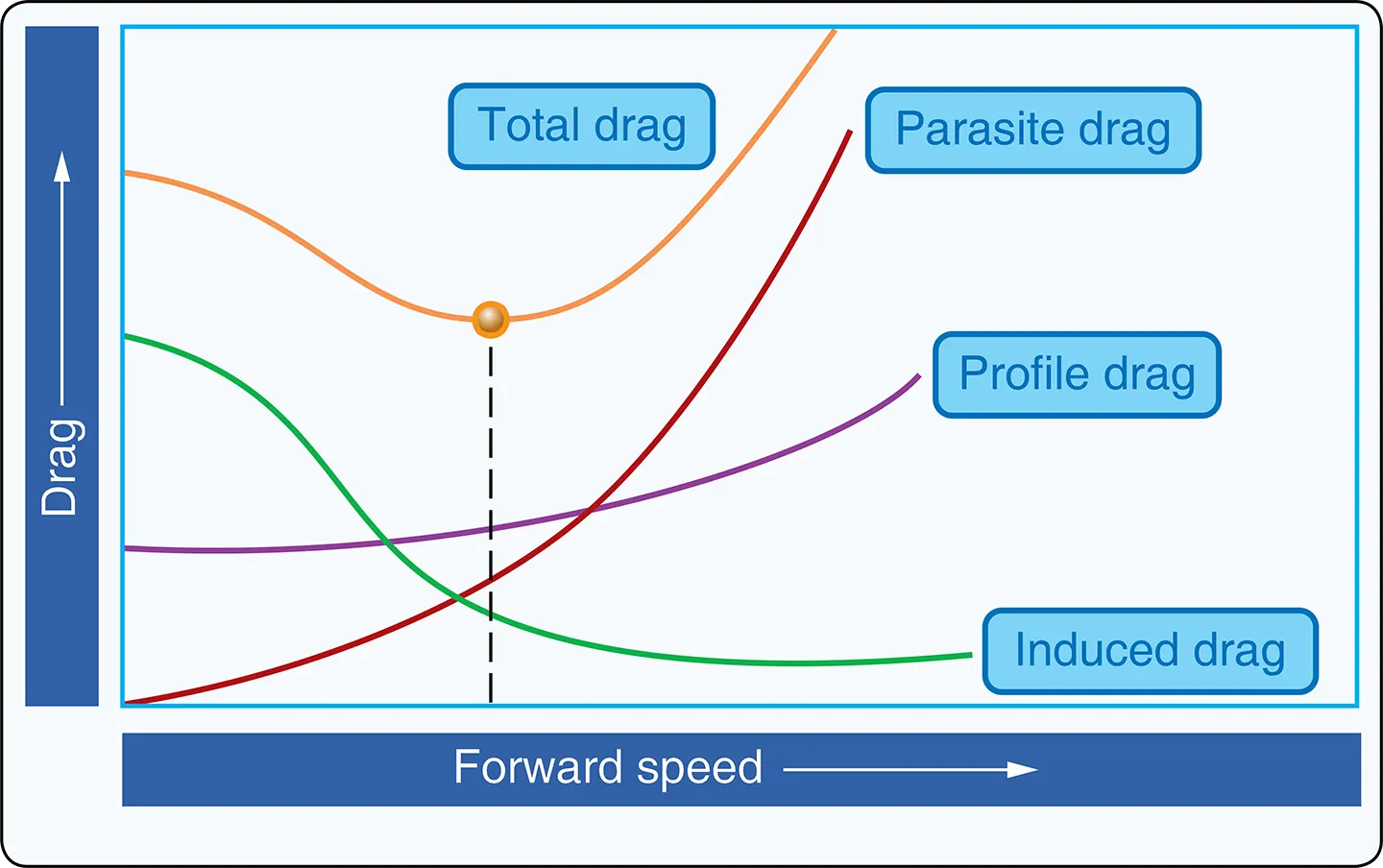
The force that resists the movement of a helicopter through the air and is produced when lift is developed is called drag. Drag must be overcome by the engine to turn the rotor. Drag always acts parallel to the relative wind. Total drag is composed of three types of drag: profile, induced, and parasite.
Profile Drag
Profile drag develops from the frictional resistance of the blades passing through the air. It does not change significantly with the airfoil’s AOA but increases moderately when airspeed increases. Profile drag is composed of form drag and skin friction. Form drag results from the turbulent wake caused by the separation of airflow from the surface of a structure. The amount of drag is related to both the size and shape of the structure that protrudes into the relative wind. [Figure 7]
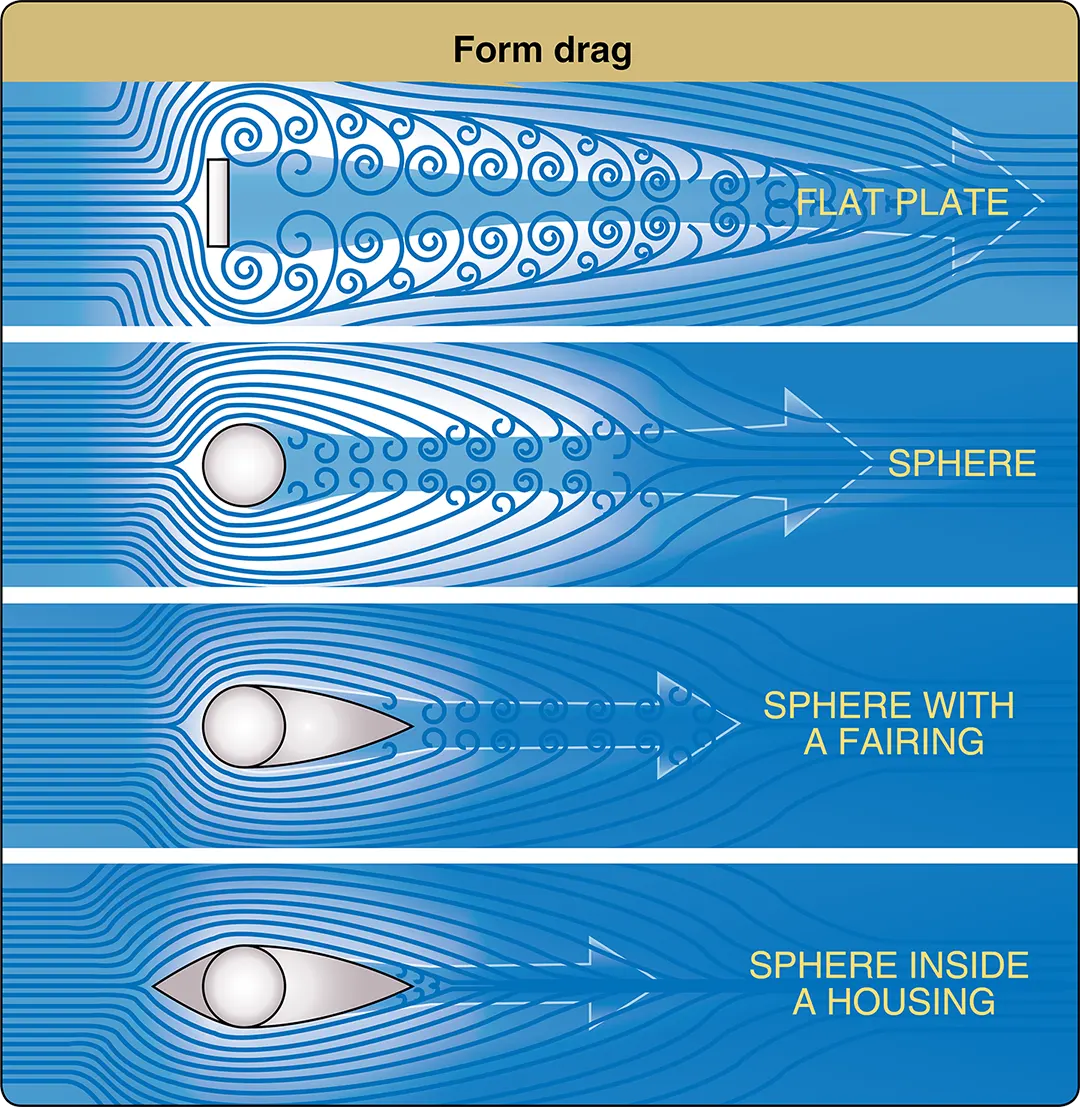
Skin friction is caused by surface roughness. Even though the surface appears smooth, it may be quite rough when viewed under a microscope. A thin layer of air clings to the rough surface and creates small eddies that contribute to drag.
Induced Drag
Induced drag is generated by the airflow circulation around the rotor blade as it creates lift. The high-pressure area beneath the blade joins the low-pressure area above the blade at the trailing edge and at the rotor tips. This causes a spiral, or vortex, which trails behind each blade whenever lift is being produced. These vortices deflect the airstream downward in the vicinity of the blade, creating an increase in downwash. Therefore, the blade operates in an average relative wind that is inclined downward and rearward near the blade. Because the lift produced by the blade is perpendicular to the relative wind, the lift is inclined aft by the same amount. The component of lift that is acting in a rearward direction is induced drag. [Figure 8]
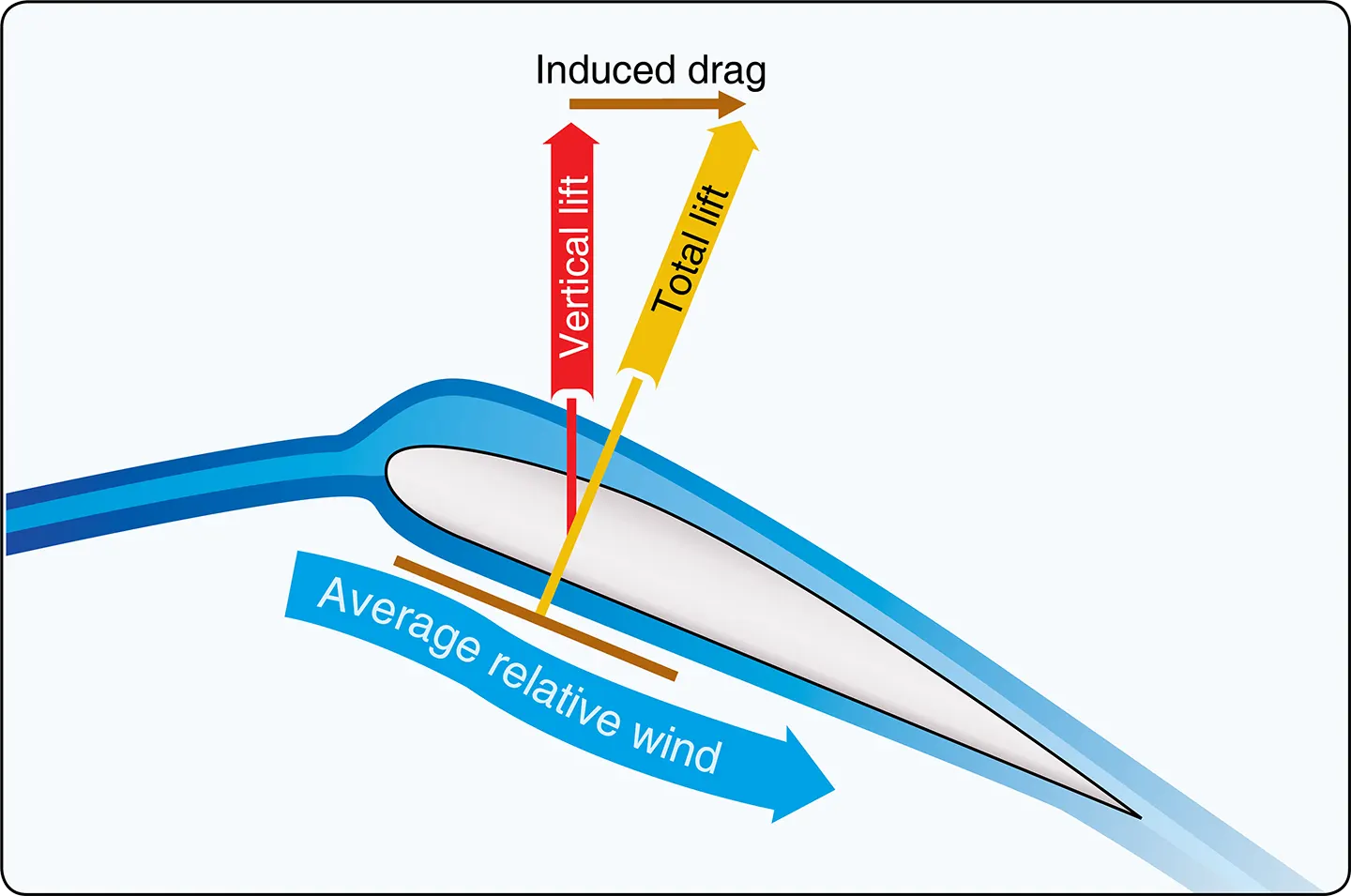
As the air pressure differential increases with an increase in AOA, stronger vortices form, and induced drag increases. Since the blade’s AOA is usually lower at higher airspeeds, and higher at low speeds, induced drag decreases as airspeed increases and increases as airspeed decreases. Induced drag is the major cause of drag at lower airspeeds.
Parasite Drag
Parasite drag is present any time the helicopter is moving through the air. This type of drag increases with airspeed. Non-lifting components of the helicopter, such as the cabin, rotor mast, tail, and landing gear, contribute to parasite drag. Any loss of momentum by the airstream, due to such things as openings for engine cooling, creates additional parasite drag. Because of its rapid increase with increasing airspeed, parasite drag is the major cause of drag at higher airspeeds. Parasite drag varies with the square of the velocity; therefore, doubling the airspeed increases the parasite drag four times.
Total Drag
Total drag for a helicopter is the sum of all three drag forces. [Figure 9] As airspeed increases, parasite drag increases, while induced drag decreases. Profile drag remains relatively constant throughout the speed range with some increase at higher airspeeds. Combining all drag forces results in a total drag curve. The low point on the total drag curve shows the airspeed at which drag is minimized. This is the point where the lift-to-drag ratio is greatest and is referred to as L/DMAX. At this speed, the total lift capacity of the helicopter, when compared to the total drag of the helicopter, is most favorable. This is an important factor in helicopter performance.